
Problemas de Cálculo de Días y Fechas y Sus Soluciones
Los cálculos de días y fechas suelen generar confusión. Los años bisiestos, los días sobrantes y los meses de distinta duración hacen que contar manualmente sea poco fiable.
Muchos buscan este tema para entender la lógica correcta y obtener explicaciones paso a paso. El objetivo es la precisión, no memorizar fórmulas ni adivinar resultados.
Esta guía presenta los cálculos de días y fechas de forma simple y estructurada. Cubre los conceptos básicos del calendario, la lógica de las fechas y métodos prácticos para resolver problemas de manera confiable.
Conceptos Fundamentales de Días y Fechas
Los cálculos de días y fechas dependen de la estructura del calendario. Sin comprender las reglas básicas, incluso problemas simples pueden resultar confusos.
Esta sección explica los principios clave para calcular días que forman la base de todos los cálculos de días y fechas.
Días de la Semana
La semana tiene 7 días que se repiten en orden fijo:
Todos los cálculos de fechas avanzan o retroceden dentro de este ciclo. Como el patrón se repite cada siete días, la cuenta siempre se realiza en múltiplos de siete.
Días de los Meses
Cada mes tiene un número fijo de días, excepto febrero. Conocer la duración de los meses es esencial para calcular diferencias de fechas y cambios de día:

El número de días por mes afecta directamente los cálculos de días sobrantes y las transiciones de fechas.
Tipos de Años
Un año se clasifica según la cantidad de días que contiene:
Un año común añade un día al ciclo del calendario, mientras que un año bisiesto añade dos.
Comprender este patrón repetitivo ayuda a predecir días pasados y futuros con precisión.

Problemas y Soluciones de Cálculo de Años Bisiestos
Los años bisiestos suelen generar confusión porque febrero tiene 29 días en lugar de 28. Este pequeño cambio afecta los cálculos de fechas, la predicción de días y la planificación.
Ignorar los años bisiestos puede causar errores en horarios, recordatorios de cumpleaños, plazos de trabajo y cálculos históricos de fechas.
Problemas y Soluciones en la Vida Real
Problema 1: Verificar si un año es bisiesto
Muchas personas no saben si un año específico es bisiesto.
Problema 2: Calcular la Edad Correctamente
Si alguien nació el 29 de febrero, calcular su edad puede ser complicado.
Problema 3: Planificar Eventos Futuros
Ignorar los años bisiestos puede causar errores al programar eventos anuales como aniversarios o contratos.
Problema 4: Encontrar el Día de una Fecha Pasada
Al calcular el día de la semana de eventos históricos, omitir los años bisiestos suele dar resultados incorrectos.
Concepto de Días Sobrantes y Problemas
Los días sobrantes son una de las principales causas de errores en los cálculos de fechas.
Muchas personas no encuentran el día correcto de la semana porque desconocen cómo los días extra de las semanas afectan el cálculo.
Comprender los días sobrantes facilita encontrar días de la semana pasados o futuros, calcular cumpleaños y aniversarios o planificar eventos.
¿Qué son los días sobrantes?
Los días sobrantes son los días que quedan después de contar semanas completas.

Problemas y Soluciones en la Vida Real
Problema 1: Predecir el Día de la Semana para una Fecha Futura
Muchas personas no pueden determinar rápidamente qué día de la semana será después de un número determinado de días.
Problema 2: Calcular los Días Entre Dos Fechas
Contar cada día manualmente es confuso y propenso a errores si no se usan los días sobrantes.
Encontrar el Día de la Semana para una Fecha Dada
A muchas personas les resulta difícil saber qué día de la semana cae una fecha específica.
Contar manualmente suele generar errores, especialmente para fechas pasadas o futuras. Usar un método paso a paso con días sobrantes facilita encontrar el día correcto.
Método Paso a Paso
Ejemplo de Problema
Pregunta: ¿Qué día fue el 15 de agosto de 1947?
Respuesta: Viernes

Encontrar la Fecha a Partir de un Día de la Semana
A veces conocemos el día de la semana, pero necesitamos hallar la fecha exacta. Esto puede ser confuso al planificar eventos, reuniones o actividades personales.
Sin un método adecuado, es fácil cometer errores y obtener la fecha incorrecta.
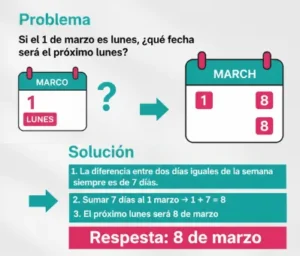
Problema y Solución en la Vida Real
Problema: Si el 1 de marzo es lunes, ¿qué fecha será el próximo lunes?
Estos cálculos no requieren fórmulas complejas. Contar cuidadosamente y comprender el ciclo semanal es suficiente para encontrar la fecha correctamente.
Más información: Plantillas de Excel para calcular días con fórmulas
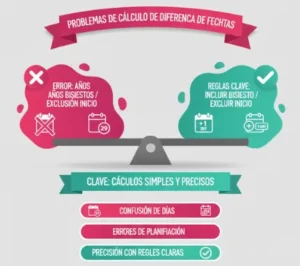
Problemas de Cálculo de Diferencia de Fechas
Encontrar el número de días entre dos fechas es una causa común de confusión.
A menudo se cuentan mal los días, se olvidan los años bisiestos o se usan diferentes formatos de fecha, lo que genera errores en planificación, programación o cálculo de duraciones.
Conocer las reglas hace que estos problemas sean simples y precisos. Reglas Clave

Problemas y Soluciones en la Vida Real
Más información: Consejos prácticos para el cálculo preciso de días y fechas
Problemas de Cálculo de Días Pasados y Futuros
Calcular días en el pasado o en el futuro puede resultar complicado. Muchas personas se equivocan al planificar eventos, plazos o viajes.
Usar un método simple de división facilita encontrar rápidamente el día correcto de la semana.
Problemas y Soluciones en la Vida Real
Problema 1: Si hoy es miércoles, ¿qué día será dentro de 45 días?
Problema 2: Si hoy es viernes, ¿qué día fue hace 18 días?
Problemas de Razonamiento Lógico Basados en el Calendario
Algunos problemas de fechas combinan el conocimiento del calendario con el razonamiento lógico.
Muchas personas se confunden al calcular el día de la semana para fechas muy separadas dentro del mismo mes o año. Usar divisiones simples y residuos hace que estos problemas sean fáciles de resolver.
Problema y Solución en la Vida Real
Problema: Si el día 5 de un mes es domingo, ¿qué día será el 25?

Problemas Avanzados de Días y Fechas
Algunos problemas de fechas son más complejos porque involucran varios años bisiestos, cambios entre meses y años o períodos largos de tiempo.
Si no se aplican correctamente las reglas de años bisiestos y días sobrantes, pueden generar confusión. El uso de un conteo sistemático los hace sencillos.

Problema y Solución en la Vida Real
Problema: ¿Qué día será el 1 de enero de 2101, sabiendo que el 1 de enero de 2001 fue lunes?
Técnicas Rápidas para el Cálculo de Días y Fechas
Calcular días y fechas manualmente puede llevar tiempo. Usar técnicas rápidas simplifica el proceso y mejora la precisión.
Estos métodos funcionan para cualquier año y permiten encontrar rápidamente el día de la semana de una fecha determinada.
Códigos de Mes (Año No Bisiesto)
Cada mes tiene un código que facilita los cálculos. En años bisiestos, se debe sumar 1 adicional para enero y febrero.
Códigos de Siglo
Los códigos de siglo ayudan a ajustar los cálculos según el siglo correspondiente:
Ejercicios Prácticos con Soluciones
Esta sección presenta ejercicios prácticos para reforzar los conceptos de días y fechas explicados anteriormente. Cada problema está diseñado para mejorar la precisión y la rapidez en los cálculos, aplicando reglas claras y métodos lógicos en situaciones reales.
Conclusión Final
Los problemas de cálculo de días y fechas son sencillos cuando se dominan los conceptos básicos.
Este tema evalúa principalmente el razonamiento lógico, la precisión y la constancia, más que las matemáticas avanzadas. Comprender años bisiestos, días sobrantes y atajos acelera la resolución.
La práctica regular y la revisión de reglas clave fortalecen la exactitud y la velocidad. Aplicar métodos de forma consistente convierte este tema en una ventaja clara en exámenes y en el razonamiento diario.
Con explicaciones claras, ejemplos resueltos y ejercicios prácticos, esta guía ofrece un recurso completo. Cubre desde lo básico hasta lo avanzado para dominar el cálculo de días y fechas con confianza.






